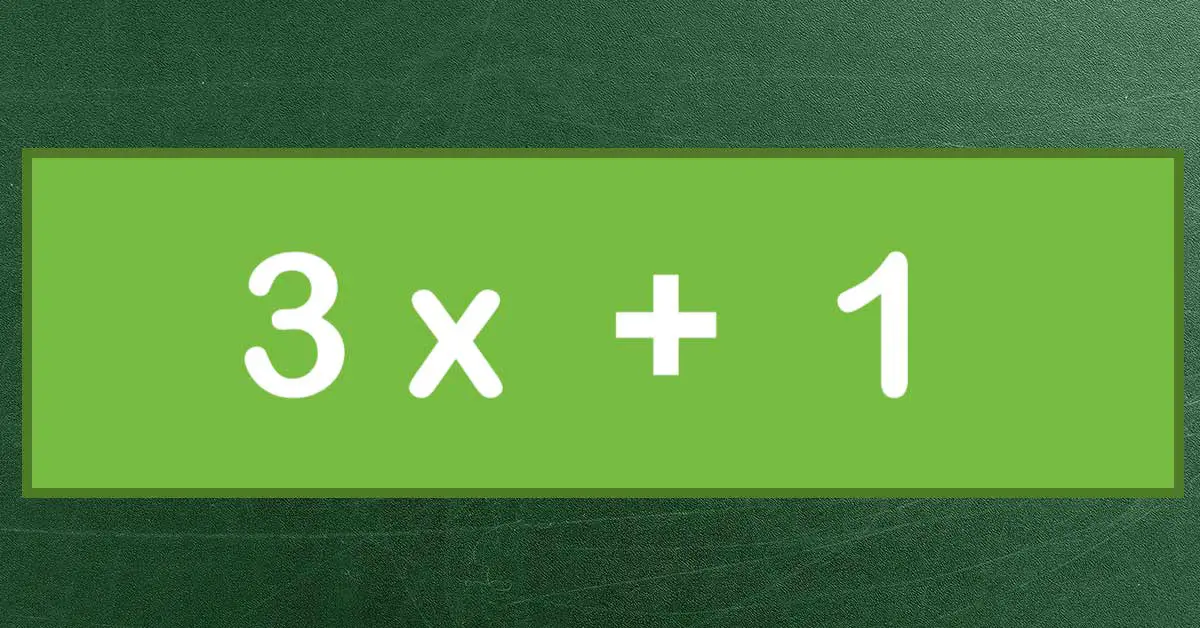It might be hard to believe but there actually exists some math problems that no one has been able to solve yet. One such math problem is known as the Collatz conjecture.
Now, before we get into the math problem, we need to understand what a conjecture is. According to the Oxford dictionary, it is “an opinion or conclusion formed on the basis of incomplete information.”[1] So with that out of the way, let us dive into what makes this conjecture so simple yet so tough.
The Origin Of The Math Problem
The conjecture is named after German mathematician Lothar Collatz. Collatz was among the most famous significant mathematicians throughout the previous century. He believed that mathematics should always take inspiration from and directly act upon phenomena in the real world. Other than the Collatz conjecture, he is also famous for being one of the founding fathers of spectral graph theory.
However, his most famous contribution is probably this conjecture. In 1937, about 2 years since he received his doctorate, he presented the Collatz conjecture. The conjecture has since been given various names. These include ‘the 3n + 1 problem’, ‘the Syracuse problem’, Hasse’s algorithm, the Thwaites conjecture, Kakutani’s problem, or the Ulam conjecture.
But even after almost 8 and a half decades since its first introduction, the conjecture remains unproven. This may make it sound daunting. But once you take a look at it you might start second-guessing. It looks really simple.
The Conjecture Out Of The Reach Of The World
The Collatz conjecture is regarding any series of numbers whose first number is a positive integer. So, let us start with a positive integer, for example, ‘x’. Then, to get the next number, there are two rules to follow:
- If ‘x’ is even, then the next number will be its half. In other words, it will be x/2.
- If ‘x’ is odd, then the next number will be 1 added to 3 times ‘x’. In other words, it will be 3x + 1. (This is also the equation that usually represents the Collatz conjecture.)
Now, we have to keep the series going until we reach 1. For example, here is an example of how it works:
Suppose x = 10. 10 is even. So the next number is 5. 5 is odd. So the next number will be 3 x 5 + 1 = 16. 16 is even, so the next number will be 16/2 = 8, and so on. If we continue like this we get the series:
10, 5, 16, 8, 4, 2, 1
See how it ended with 1? Well, this is where the conjecture starts. The conjecture states that no matter how large the starting integer is, the last number will always be 1. In other words, ‘x’ can be as big as you want it to be as long as it is a positive integer. But, if we follow these rules, we will always end up with a series whose final number is 1. Try it out with other numbers, and see for yourself.
Also, notice how the numbers in the series go higher and lower until they reach 16. This has given the name hailstone numbers or the hailstone sequence. The reason is that hailstones behave similarly when they are inside the clouds.
If you’re more of a visual person, check this video out:
So Why Is It Unsolvable?
We bet you are thinking that this is a very easy series to solve. So why is it called unsolvable even after so long?
Well, that’s because of the nature of the problem – it is a conjecture. A conjecture is only solved when it is proven. And it has been impossible, so far, to definitively prove that all positive integers when put in the Collatz series, will end at 1.
The simple reason behind why it has been so tough to prove it is because there is always a bigger number. So far, mathematicians have solved the series for numbers bigger than 200 quintillions. That is a total of 20 zeroes after 2. And the numbers have all given the same result: a sequence that ends at 1.
However, in mathematics, this does not prove that a number that has 200 zeroes after 2 will give the same result! And that’s why it has remained unsolvable. In mathematics, even if there is a single number that can counter the conjecture, it will cease to be correct.
But it is not possible to keep calculating bigger and bigger numbers. That’s why mathematicians use logical reasoning to prove such conjectures. However, we are yet to get one. The closest we have gotten to one came in 2019. Terrence Tao, one of the most brilliant mathematicians currently alive, managed to prove that 99% of all positive integers hold true for the Collatz conjecture[2].
But that’s still 99%. And Tao says that that is as close as we can humanely get to proving the Collatz conjecture. Well, we might not be able to properly solve it, but it is a lot of fun making the series out of different numbers!
Here are some more math problems for you to test your skills:
- Not Everyone Can Solve This ‘Simple’ Math Problem from the 1950s without A Calculator
- Readers Will Require Calculator To Find Solution To Complex Math Equation
- How Good Are Your Math Skills? Test Them With This Tricky Problem
Sources:
- “conjecture” Oxford Learner Dictionaries. n/d
- “Mathematician Proves Huge Result on ‘Dangerous’ Problem” Quartz. December 11, 2019